STATGRAPHICS contains extensive capabilities for the creation and analysis of statistically designed experiments. The designs that can be created are divided into several types:

1. Screening - designs intended to determine the most important factors affecting a response. Most of the designs involve only 2 levels of each factor. The factors may be quantitative or categorical. Included are 2-level factorial designs, mixed level factorial designs, fractional factorials, irregular fractions, and Plackett-Burman designs. For designs of less than full resolution, the confounding pattern is displayed. Blocking and randomization are options.

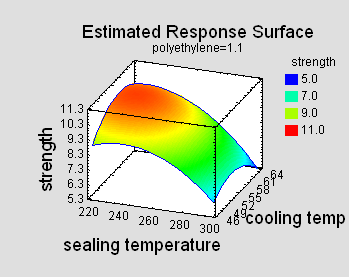
2. Response Surface - designs intended to determine the optimal settings of the experimental factors. The designs involve at least 3 levels of the experimental factors. Included are central composites, Box-Behnken designs, 3-level factorials, and Draper-Lin designs.

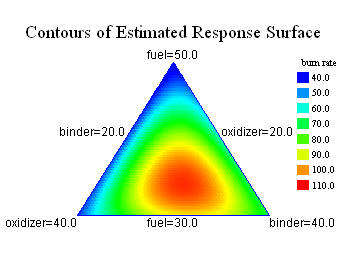
3. Mixture - designs involving components of a mixture, where the levels of the components are constrained to sum to 100% (or some other fixed value). Upper and lower constraints may be specified for each component. Included are simplex-lattice, simplex-centroid, and extreme vertices designs.

4. Multilevel Factorial - designs involving different numbers of levels for each experimental factor. These designs produce a natural candidate set for the D-Optimal design creation procedure, which will select an optimal subset of the runs.
    

5. Inner/Outer Arrays - designs consisting of both controllable and uncontrollable (noise) factors, intended to find combinations of the controllable factors at which the responses are relatively insensitive to the uncontrollable factors. Following the methods of Genichi Taguchi, both an inner and outer array are constructed.  The factors may be quantitative or categorical. As part of the analysis, signal-to-noise ratios may be constructed.
    

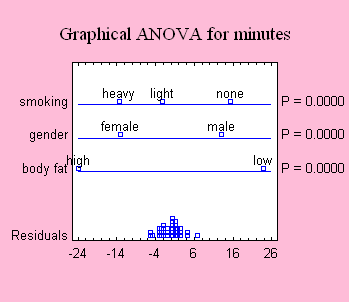
6. Single Factor Categorical - designs intended to compare levels of a single non-quantitative factor. Includes completely randomized designs, randomized block designs, balanced incomplete block (BIB) designs, Latin Squares, Graeco-Latin Squares, and hyper-Graeco-Latin Squares.

7. Multi-Factor Categorical - designs intended to study multiple non-quantitative factors, with several levels of each. Analyzed using a multifactor analysis of variance.
    

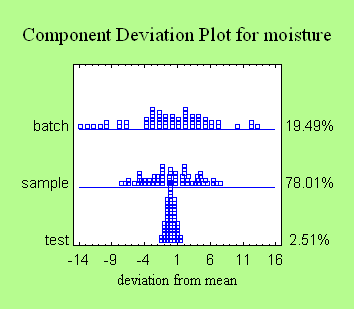
8. Variance Component (hierarchical) - designs intended to study the effect of two or more nested factors on the variability of a response. Estimates of the contribution of each factor to the overall variability are obtained.

Major Steps in Constructing and Analyzing an Experimental Design

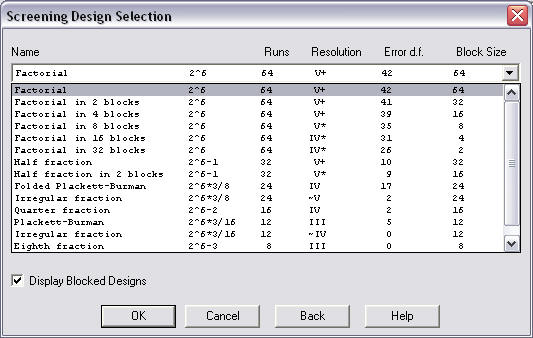
Step 1: Create Design - The experiment is created by completing a sequence of dialog boxes. On these dialog boxes, the user specifies the experimental factors and responses, the experimental region, the order of randomization, and any blocking variables.

Step 2: Perform Experiment - The selected experimental runs are then performed and the responses entered into the experiment datasheet.

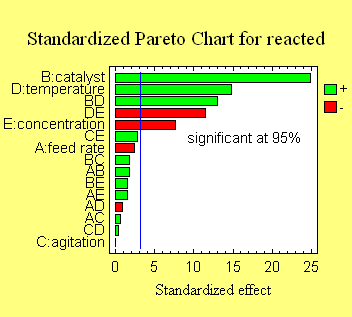
Step 3: Analyze Experiment - The response variables are analyzed and a suitable statistical model is developed. Usually, the principle of parsimony is applied to remove insignificant effects from the model.

Step 4: Augment Experiment - If necessary, additional runs are added to the initial design. STATGRAPHICS provides facilities for adding runs to resolve confounding, following the path of steepest ascent, and adding star points to convert a screening design to a response surface design.

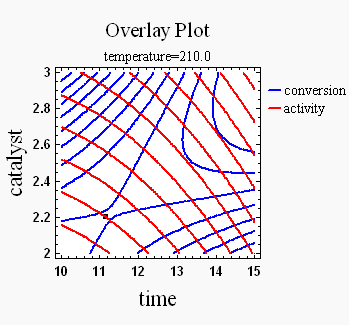
Step 5: Optimize Response(s) - Settings of the experimental factors are found that achieve the desired responses. If more than one response is present, desirability functions may be defined to combine the different goals.