The late Prof. John Tukey had a major impact on statistical data analysis. In his classic book entitled Exploratory Data Analysis, he introduced many techniques for discovering unique features contained in data. STATGRAPHICS Centurion contains several of his procedures, plus other methods designed to help extract information:

1. Box-and-Whisker Plots - five-number summaries of data samples, with optional indicators for outside points.

2. Stem-and-Leaf Displays - data tabulation created by building a graphic from the numeric values.

3. Median Polish of Two-Way Tables - a technique for discovering a common type of pattern in two-way tables.

4. Resistant Method for Fitting a Straight Line - alternative method for fitting a straight line which is resistant to the potential presence of outliers.

5. Nonlinear Smoothers for Time Series Data - resistant smoothers based on running medians.

6. Rootograms - similar to histograms but based on the square roots of class frequencies.

7. Bubble Charts - coded X-Y scatterplots where the symbol size represents the value of an additional quantitative variable.

8. Radar/Spider Plots - technique for comparing several samples of multivariate data.

9. Scatterplot Matrices - organized arrays of 2-variable scatterplots.

10. Coded Maps - maps in which states are color-coded according to the value of a selected variable.

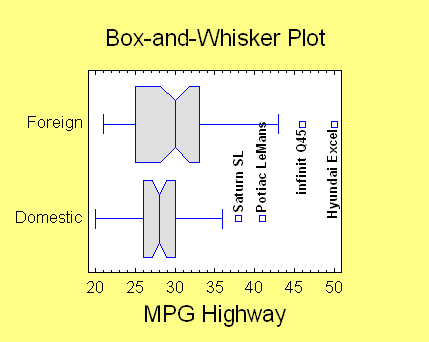
Box-and-Whisker Plots

A box-and-whisker plot is a schematic diagram that displays a five number summary of a data set based on the: minimum, lower quartile, median, upper quartile, and maximum. It is drawn with a central box that covers the middle half of the data values, a line at the median, and whiskers out to the most extreme values (unless values appear to be far away from the center, in which case they are shown as separate outside points.) If desired, notches can be added to the boxes to display the uncertainty in the location of the true population medians.

Stem-and-Leaf Displays

Tukey's stem-and-leaf display illustrates the distribution of the data values in a sample by using the leading digits from each data value to create stems and the following digits to create leaves. The digits to the right of the vertical line each represent one observation. Any unusual outside points are shown on special HI and LO stems.

Median Polish of Two-Way Tables

The Median Polish procedure constructs a model for the data in a two-way table by sweeping out column and row medians. The resulting model for the data consists of a typical value common to all cells in the table, plus specific row and column effects.

Polished Table
Sweeping 3 times.

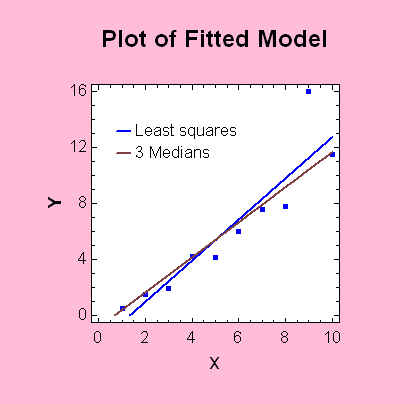
Resistant Methods for Fitting a Straight Line

When fitting a straight line, outliers can have a big impact on the fit. Tukey devised a fitting method that would be more resistant to their presence. In his method, the data are divided into three groups and the fitted line is determined from the group medians.

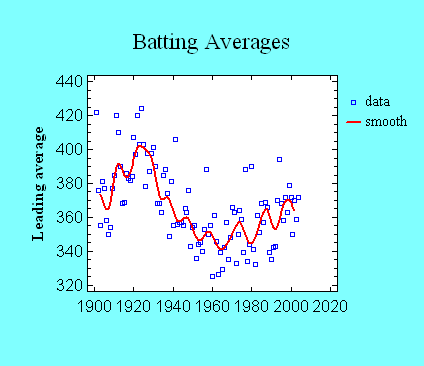
Nonlinear Smoothers for Time Series Data

Tukey's resistant nonlinear smoothers are very useful for displaying the trend in noisy time series data. In the Time Series Smoothing procedure, the smoothers are often used as preprocessors before application of a weighted moving average.

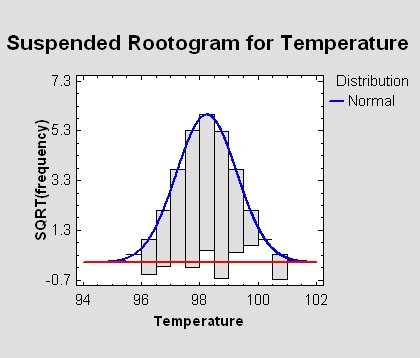
Rootograms

When assessing how closely a probability distribution matches a sample of data, standard histograms suffer from the fact that the longer bars are subject to greater sampling variability than the shorter bars. By plotting the square roots of the frequencies rather than the frequencies themselves, it is easier to see where any significant discrepancies are occurring. The visual comparison can be made even easier by suspending the bars from the curve, so that deviations between observed and expected frequencies can be judged by comparing the bars to a horizontal rather than a curved line.

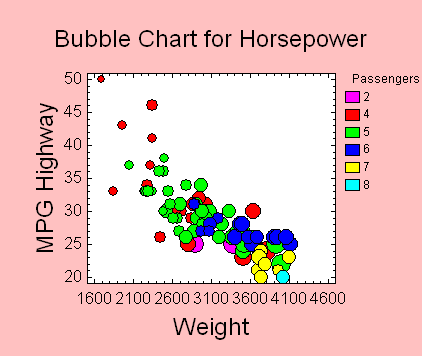
Bubble Charts

A bubble chart can be used to display four variables simultaneously: one on each of the X and Y axes, one defining the size of the bubbles, and one defining the colors.

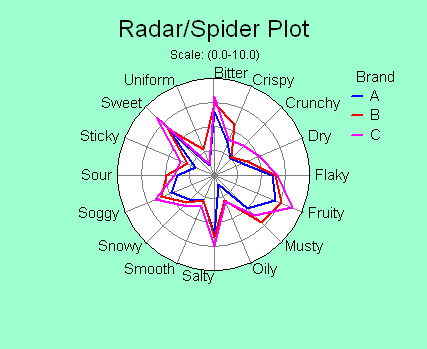
Radar/Spider Plots

When a relatively small number of samples need to be compared and the number of variables is large, a radar or spider plot can be very effective. The magnitude of each variable is shown along one of the spokes.

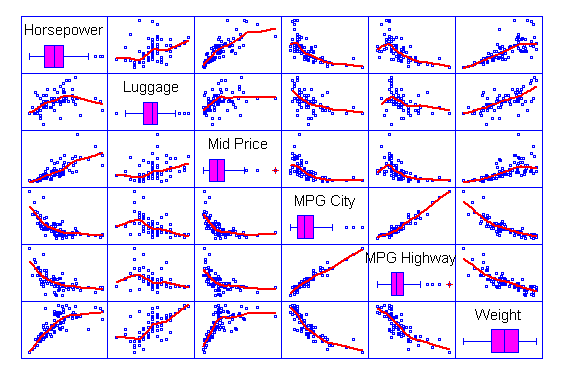
Scatterplot Matrices

A great way to display multiple quantitative variables is by creating a scatterplot matrix. Each cell of the matrix contains a plot for a selected pair of variables. All plots in any given row have the same variable on the Y axis, while all plots in a given column have the same variable on the X axis. Adding a smoother to each cell helps illustrate any relationships.

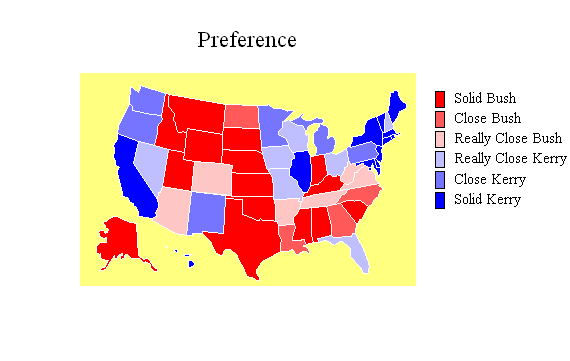
Coded Maps

Special types of plots can also be useful for displaying geographical data. The map below illustrates the results of a poll taken several months before the last U.S. presidential election.